不同的误差源如何导致偏差和方差有助于我们改进数据拟合过程,从而产生更准确的模型。三种方式定义偏差和方差:概念上,图形上和数学上。
概念上
-
Error due to Bias: 表示我们的模型预测的期望值(或者叫平均值)与模型想要努力接近真实值的difference。期望值是指,你可以通过多个数据集(随机性)来训练多个模型(参数会不同),这些模型的预测值与真实值的偏差叫Bias。不可以简单认为一个模型的多个测量算得的。
-
Error due to Variance: 表示模型对于给定数据点预测的可变性。当然可变性的统计也是基于一系列模型产生的。Variance是对于给定点的预测在模型的不同实现之间的变化性。
图形上
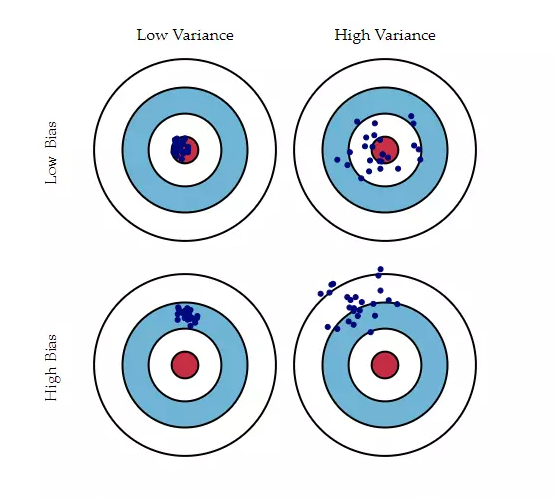
数学上
假设预测值 $Y$ 与协变量 $X$ 之间满足 $Y=f(X) + \epsilon$, 误差项 $\epsilon$ 以0为均值的正态分布,$\epsilon \backsim N(0, \sigma_{\epsilon})$.
我们用线性模型或者其他模型估测$f(X)$的模型$\hat{f}(X)$, $x$点处的预期平方预测误差为:
$$
Err(x) = E\lbrack(Y - \hat{f}(x))^2\rbrack
$$
然后可以将该错误分解为偏差和方差分量:
$$
Err(x) = (E[\hat{f}(x)] - f(x))^2 + E[(\hat{f}(x) - E[\hat{f}(x)])^2] + \sigma_{e}^2
$$
$$
Err(x)=Bias^2 + Variance + Irreducible Error
$$
$Irreducible Error$ 是真实关系中的噪声项,任何模型都不能从根本上减少。
鉴于真实模型和无限数据来校准它,我们应该能够将偏差和方差项减少到0.然而,在一个模型不完善和数据有限的世界中,在最小化偏差和最小化方差之间存在权衡。
参考
Understanding the Bias-Variance Tradeoff