逻辑回归 Logistic Regression

概念

根据现有数据对分类边界线(Decision Boundary)建立回归公式，以此进行分类。用于估计某种事物的可能性。用的是“可能性”，而非数学上的“概率”，logisitc回归的结果并非数学定义中的概率值，不可以直接当做概率值来用。该结果往往用于和其他特征值加权求和，而非直接相乘。

逻辑回归与线性回归的关系

相同点：逻辑回归与线性回归都是一种广义线性模型。去除Sigmoid映射函数的话，逻辑回归算法就是一个线性回归。
不同点：逻辑回归假设因变量 y 服从伯努利分布，而线性回归假设因变量 y 服从高斯分布。

逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

数学理论

Sigmoid函数，也称为逻辑函数（Logistic function）：
$$
g(z) = \frac{1}{1 + e^{-z}}
$$
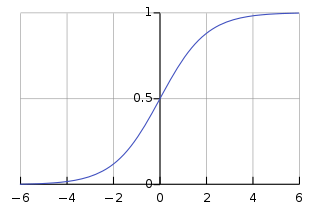
Sigmoid
sigmoid函数是一个s形的曲线，它的取值在[0, 1]之间，在远离0的地方函数的值会很快接近0或者1。它的这个特性对于解决二分类问题十分重要。

逻辑回归的假设函数为：
$$
h_{\theta}(x) = g(\theta^Tx),
g(z) = \frac{1}{1 + e^{-z}}
$$
所以，
$$
h_{\theta}(x) = \frac{1}{1 + e^{-\theta^Tx}}
$$
其中 $x$ 是我们的输入，$\theta$ 为我们要求取的参数.
逻辑回归模型所做的假设是:
$$
P(y=1|x;\theta) = g(\theta^Tx) = \frac{1}{1 + e^{-\theta^Tx}}
$$
即在给定 $x$ 和 $\theta$ 的条件下 $y=1$ 的概率，
$g(h)$ 就是上面提到的sigmoid函数, 与之相对应的决策函数为：
$$
y^* = 1, if P(y=1|x) > 0.5
$$
实际应用时特定的情况可以选择不同阈值，如果对正例的判别准确性要求高，可以选择阈值大一些，对正例的召回要求高，则可以选择阈值小一些。

评估指标

最常用的是代价函数是交叉熵(Cross Entropy), 交叉熵是对「出乎意料」的度量. 交叉熵衡量的是我们在知道y的真实值时的平均「出乎意料」程度。当输出是我们期望的值，我们的「出乎意料」程度比较低；当输出不是我们期望的，我们的「出乎意料」程度就比较高。
$$
J(\theta) = -\frac{1}{m}[\sum_{i=1}^m (y_{(i)}logh_{\theta}(x^{(i)}) + (1 - y^{(i)}log(1 - h_{\theta}(x^{(i)})))]
$$

$m$训练样本的个数, $h_{\theta}(x^{(i)})$ 用参数 $\theta$ 和 $x$ 预测出来的 $y$值, $y$ 原训练样本中的 $y$ 值，也就是标准答案, 上角标 ${i}$ 第 ${i}$ 个样本

ScikitLearn 中的逻辑回归用法

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 101)
logmodel = LogisticRegression()
logmodel.fit(X_train, y_train)
predictions = logmodel.predict(X_test)

print(classification_report(y_test, predictions))
confusion_matrix(y_test, predictions)

混淆矩阵 Confusion Matrix

n=165	Predicted: NO	Predicted: Yes
Actual: NO	TN=50	FP=10	60
Actual: Yes	FN=5	TP=100	105
	55	110

TP: True Positives
TN: True Negatives
FP: False Positives (Type I error)
FN: False Negatives (Type II error)

正确率为：
$$\frac{TN + TP}{total} =\frac{50+100}{165}$$
错误率为：
$$\frac{FP + FN}{total} =\frac{5+10}{165}$$

数学知识补充

伯努利分布亦称“零一分布”、“两点分布”。称随机变量X有伯努利分布, 参数为p($0 < p < 1$) 如果它分别以概率p和1-p取1和0为值。$E(X)=p$, $D(X)=p(1-p)$。

参考

逻辑回归（Logistic Regression)（一）

概念