决策树与随机森林

决策树概念

决策树实际上是将空间用超平面进行划分的一种方法，每次分割的时候，都将当前的空间一分为二。

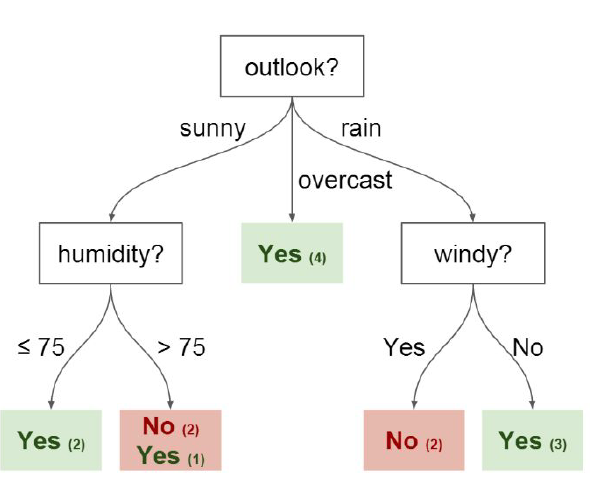
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点（node）和有向边（directed edge）组成。结点有两种类型：内部结点（internal node）和叶结点（leaf node）。内部结点表示一个特征或属性(features)，叶结点表示一个类(labels)。

• 结点：根据某一属性值拆分数据
• 边：拆分结果到下一个结点
• 根结点：执行第一次拆分的结点
• 叶子结点：终端节点，预测结果
  

随机森林概念

是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。

随机森林的构造过程

1. 假如有N个样本，则有放回的随机选择N个样本(每次随机选择一个样本，然后返回继续选择)。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。
2. 当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。
3. 决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
4. 按照步骤1~3建立大量的决策树，这样就构成了随机森林了

随机森林随机性

随机森林对输入的数据的行,列进行随机采样:

• 对于行采样，采用有放回的方式，也就是在采样得到的样本集合中，可能有重复的样本。假设输入样本为N个，那么采样的样本也为N个。这样使得在训练的时候，每一棵树的输入样本都不是全部的样本，使得相对不容易出现over-fitting。
• 列采样，从M个feature中，选择m个（m << M）
  两个随机采样的过程保证了随机性，所以就算不剪枝，也不会出现over-fitting

随机森林的优点

1. 在数据集上表现良好，随机森林不容易陷入过拟合
2. 随机森林具有很好的抗噪声能力
3. 够处理很高维度（feature很多）的数据，并且不用做特征选择
4. 既能处理离散型数据，也能处理连续型数据，数据集无需规范化
5. 可生成一个$Proximities=p_{ij}$矩阵，用于度量样本之间的相似性： $p_{ij}=\frac{a_{ij}}{N}$, $a_{ij}$表示样本i和j出现在随机森林中同一个叶子结点的次数，N随机森林中树的颗数
6. 创建随机森林的使用的是无偏估计
7. 训练速度快
8. 训练过程中能够检测到feature间的互相影响
9. 容易做成并行化方法
10. 实现简单

信息熵 & 信息增益 & 信息增益率

• 信息熵(Information Entropy)
  $$
  Ent(D) = -\sum_{k=1}^{|y|}p_{k}log_{2}p_{k}
  $$
  $|y|$ 表示类别的个数，信息熵越小的话，表明这个数据集越纯粹，即类别越少。$Ent(D)=0$,则数据集中只有一个类别

• 条件熵
  条件熵表示在条件X下Y的信息熵
  $$
  Ent(Y|X)=\sum_{x \in X}p(x)H(Y|X=x)
  $$

• 信息增益(Information Gain)
  信息增益 = 信息熵 - 条件熵

• 信息增益率(Information Gain Ratio)

ScikitLearn 中决策树

1
2
3
4
5
6
7
8
9
10
11
12
13
14

from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report, confusion_matrix

X = df.drop('Kyphosis', axis = 1)
y = df['Kyphosis']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
dtree = DecisionTreeClassifier()
dtree.fit(X_train, y_train)
predictions = dtree.predict(X_test)
from sklearn.metrics import classification_report, confusion_matrix

print(classification_report(y_test, predictions))
print(confusion_matrix(y_test, predictions))

ScikitLearn 中随机森林

1
2
3
4
5
6
7
8
9

from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix

rfc = RandomForestClassifier(n_estimators=200)
rfc.fit(X_train, y_train)
rfc_pred = rfc.predict(X_test)
print(classification_report(y_test, rfc_pred))
print(confusion_matrix(y_test, rfc_pred))

参考链接

说说随机森林

• ← Previous Post
• Next Post →